
Six children are in a classroom, their faces beaming and their laughter echoing through the surrounding halls. Some of them are jumping up and down. Another is excitedly reciting multiplication facts. The remaining few are seated, their pencils rapidly scratching lopsided numbers across fresh sheets of paper.
On most days, the Pasquerilla Center is full of Notre Dame’s ROTC members, hard at work. But, on Tuesday and Wednesday evenings, its classrooms become a math lover’s playground and these children, who have just completed their first “wiggle worm” puzzle, are its eager visitors.

They are participating in the Riverbend Math Circles at Notre Dame, brought to campus by Amanda Serenevy, Ph.D., executive director of the Riverbend Community Math Center. The center has maintained a years-long partnership with the University’s Department of Mathematics, which continued this fall when the center’s math circles were moved to campus with the assistance of Sonja Mapes-Szekelyhidi, associate professor of the practice and director of undergraduate studies in the Department of Mathematics.
Serenevy uses her circles to fight what she has deemed “mathphobia,” a fear of math often formed by the cumulative nature of the subject. Many students who struggle with basic concepts accept the label “bad at math.” As math builds upon itself, these concepts never go away, and their fear is perpetuated by the rigidity of traditional mathematics instruction.
“Math circles, at least the tradition that I’m in, are trying to engage students in a community of mathematical thinkers and problem solvers,” Serenevy explained. “We’re making sure that we’re allowing our students to actually be creative with math, which means they get to see the fun part, as opposed to just following the rules.”
By creating a positive math-learning environment from an early age, Serenevy hopes to empower her students to love mathematics and their unique ways of approaching it. She believes that fostering a dynamic relationship with math now will help students continue their study of the subject, especially as they move onto complex topics.

Math circles are after-school groups for K-12 students to engage with skilled mathematicians in a casual fashion. They originated in Bulgaria during the early 20th century and did not make their way to the United States until 1994, when Robert and Ellen Kaplan formed the Boston Math Circle in response to “poor quality and low level of math education in the United States.” The Kaplans’ circle began with 29 students and quickly grew. At one point, it included Serenevy, when she was working towards her doctoral degree at Boston University. She credits her time in the Boston circle with her decision to start Riverbend in 2006.
“I was thinking originally of being a professor and doing outreach on the side, but then I decided that the outreach was so much more interesting to me and I really wanted that to be my main career,” she said.
Serenevy has committed herself to improving math accessibility through her work at Riverbend. She wants to empower all students, regardless of family income and background, so the center provides its unique STEM opportunities, including math circles, free of charge.
The circles, each named for a mathematician--Galois, Germain, Wiles, and Euler--serve children ages 4-18. The groups are divided by age and each meets weekly, for an hour in the Pasquerilla Center on Notre Dame’s campus. As part of the new partnership with the math department, circles are led by undergraduate and graduate students who have enrolled in Mapes’ 2-credit course about math circle theory. They learn about the philosophy behind the circles and about how to teach a math circle problem.
Instead of traditional math problems, math circles utilize low-threshold, high-ceiling problems--those that are not overly difficult to solve on the surface, but can be explored more deeply to reveal complex principles. For younger students, this currently means playing fun games like “wiggle worms” and, for older students, this currently means studying ancient counting systems and writing theoretical papers about them. The problems challenge traditional thinking, and their solutions require students to think deeply and uncover hidden math theory and concepts.
Because it may be difficult to understand a math circle without experiencing one, here is an example of a basic circle activity: wiggle worms.
Wiggle worms are one of the first activities young math circlers participate in. They set a foundation for the rest of the program and introduce the math circle methodology:
The activity begins with a grid, 5x5 in most cases.
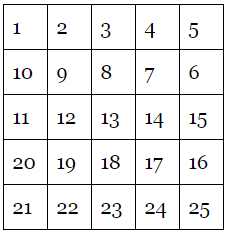
Children are told to write a 1 in a top corner box and tasked to count up to 25, placing the next number in an adjacent box without skipping any numbers or jumping over any boxes.
Naturally, most of them produce a grid like this:
They then draw a swirl through the numbers to show the path they took:
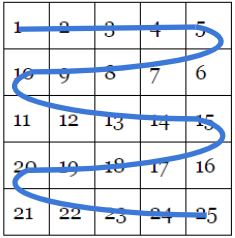
And the resulting swirly shape is the wiggle worm.
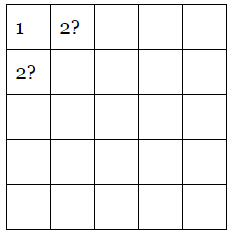
Pretty easy counting game, right? But next, students are asked to make a worm that starts in this box:
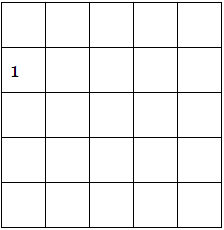
When they start, they might think they can do it. They’ll try several combinations, and eventually they’ll come close to the end and realize they can’t finish the worm.
But, why?
This is what the children are trying to figure out. They have drawn empty 2x2, 3x3, 4x4 and 5x5 grids on the chalkboard and refer to them as their “data.” They each choose a square from a grid and attempt to begin a wiggle worm in that square. If they are able to complete the worm, they draw a check in the box. If not, they draw a question mark. And repeat.
Alex Kokot, a Notre Dame junior who helps lead the math circles, says that the data collection helps the kids to see the pattern, which ultimately leads them to the proof.
If each check was represented by a black square and each question mark represented by an empty box, their data would look like this:




“Instead of seeing it as just a grid, you can see it as kind of a chessboard,” Kokot said. He explained that the 5x5 grid has 25 squares--13 black and 12 white. To make a wiggle worm, you must move to a black square if you’ve been in a white one and vice versa. This means that it will be impossible to begin a worm in any white square of a grid with an odd number of spaces because there will always be too many black squares for you to finish. It also means that a worm can be started in any space of any grid with an even number of squares.
This example clearly demonstrates the way that the circle functions--what feels like a fun math puzzle is actually a deep proof of a concept that is integral to the subject--the concept of odd and even numbers.
The excitement that comes from solving the puzzle leads many of the young students to cheer and clap. It’s clear that they have fallen in love with math.
Serenevy’s mission to improve STEM access and excitement aligns with Notre Dame’s mission to act as a “force for good in the world.” For the spring semester of 2020, she will no longer lead the circles, as Professor Mapes and the students she has trained will be taking over.
“I’m so excited that we have this partnership that Professor Mapes has made possible,” Serenevy said. “I’m going to go on sabbatical in the spring and they’re going to run it all.”
During her sabbatical, Serenevy plans to write new curriculum for Riverbend, so she can continue to expand her mission and help more young people discover the joy of math.